Compilers | Kabilan Mahathevan

Introduction
- Things I should know
- Where do I start
Grammar

Introduction

Compilers are human-machine translators that transform human-readable code into machine-readable programs. Compilers are like our intelligent friend who speaks multiple languages and helps us get around in a foreign country. You don’t need to learn the foreign language to explore the city, you only need to develop the skills to communicate properly with your intelligent friend and make him do whatever you want (not intended in a manipulative way! maybe just a little). We’ve spent around 70 years developing the perfect compiler, and we still haven’t reached a mature stage, because there’s no perfect way to communicate with your friend in all scenarios.

I’m personally an introverted person, which means it has always been very difficult for me to make new friends. I still have friends who have been with me for more than 15 years. Now, I’ve decided to learn how to make new friends, and the first step is to develop my communication skills. As the first part of that journey, I’m going to learn how to talk to a computer, just like any nerdy, introverted person would do. No, it’s not about LLMs, because I don’t want to learn English to speak with a Chinese person. I’m going to build a compiler while learning about its intricate parts and technical details.

What a weird way to start a project! I’m going to use this as an entry for record-keeping.

Things I should know

How to take all the English letters, numbers, and symbols—and make sense of them.
How to map what each letter, number, or symbol means—and how to even understand what counts as a number versus an English character.
What machine code is, and what it looks like.
How to turn all of my program code into machine code.
How the compiler knows that I’ve made a mistake in the program before converting it into machine code.

So, what do I know as I start this record? Nothing! Just a few tiny details about compilers, thanks to my experience using different compilers for C/C++ projects. What an idiot I am! I’ve been using compilers for so long without even making an effort to understand how they work.

Where do I start

The main part of learning is asking the right questions and knowing what you don’t know. So my first question is: How do we take all the English letters, numbers, and symbols—and make sense of them?

It’s just like learning a new language. You always start with grammar. So I’m also going to start with the concept of grammar and how it helps answer Question 1.

Grammar

Grammar is the set of rules that define how words are arranged to form meaningful sentences in a language. Its purpose is to ensure clear and consistent communication by organizing words in a structured, understandable way. Therefore, to build any programming language that compilers can understand, we first have to define its grammar. Again, a question arises: What does grammar look like? Does it have verbs or subjects, like in natural languages? To understand this, we need to formally define what a formal grammar looks like in the context of a programming language.

I remember studying something like this during my undergraduate Theory of Computation class. It’s time to refresh that memory.

A formal grammar is a mathematical specification of a language’s syntax, typically defined as a 4‑tuple G=(N,Σ,P,S) where N is a finite set of nonterminal symbols, Σ a set of terminal symbols (disjoint from N), P a set of production rules, and S ∈ N the start symbol

Oh! That’s a lot to digest. I don’t even know what this means at this point. Let’s break it down, part by part, and understand all the small details to fully grasp what it really means.

A formal grammar is a mathematical specification of a language’s syntax
Syntax refers to the specific rules that dictate the structure and arrangement of symbols and words in a programming language. Therefore, mathematically specifying this syntax is what is defined as a formal grammar.
typically defined as a 4‑tuple G=(N,Σ,P,S)
Grammar is formally defined as a tuple of four elements, each specifying a set of features/rules of a programming language.
N is a finite set of nonterminal symbols.
There are a lot of things in this small sentence. Let's break it down. First, what are non-terminal symbols?, what other symbols are there?, why does it have to be finite? and what does finite mean?
1. what are non-terminal symbols?, what other symbols are there?
  When writing grammar rules, we use two types of symbols: non-terminal symbols and terminal symbols. Terminal symbols are the actual characters or tokens that appear in your program and cannot be broken down any further.
  
  A few examples of non-terminal symbols in a Python-like programming language are:
```
if, else, print, (, ), +, -, identifier, number
```
  Non-terminal Symbols are placeholders for patterns or structures made up of terminals or other non-terminals.
```
print(3+5)
```
  Let’s take the above as a simple program written in our own programming language. Now, let’s see how the terminals and non-terminals would make up the grammar.
```
Program    --> Statement
Statement  --> "print" "(" Expression ")"
Expression --> Term "+" Term
Term       --> number
```
  Here, our Program is print(3+5), which is a non-terminal symbol. According to our grammar, it is made up of terminal symbols such as print, (, and ), and a non-terminal symbol called Expression. The Expression here represents 3+5, which is itself a combination of the terminal symbol + and non-terminal symbols like Term. Term is a non-terminal symbol that ultimately represents a terminal symbol, number. Refer the image below for better clarity.
  
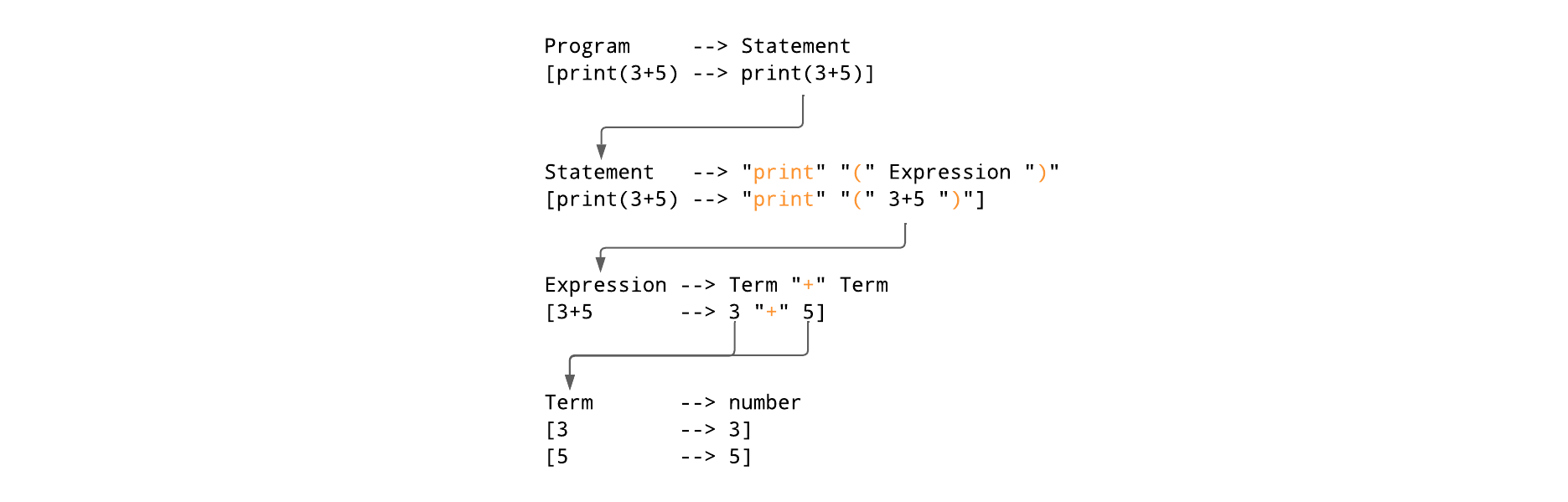
  Each statement in the grammer above is also known as Production and these statements are also know as Production Rules We will look into this later.
2. why does it have to be finite?
  Computers (and compilers) are finite machines. They can only hold and process finite amounts of data. If we have infinite number of non-terminals
Σ a set of terminal symbols (disjoint from N)
We’ve already understood what terminal symbols are, but what does disjoint from NM mean? N is the set of non-terminal symbols, as we’ve seen before, and the set of terminal symbols Σ cannot contain any elements from N. This implies that N and Σ are disjoint sets, they have no elements in common.
P a set of production rules
A production (also called a production rule) is a single rule within the grammar that tells how a non-terminal can be replaced (or "expanded") into a sequence of terminals and/or other non-terminals. We have already looked at an example of a set of productions. Consider the earlier example: print(3+5). We can define a production rule to read the program as follows:
```
Program    --> Statement
Statement  --> "print" "(" Expression ")"
Expression --> Term "+" Term
Term       --> number
```
These are what we call production rules.
S ∈ N the start symbol
S is one of the important specification which indicates the starting point of any scan operations. Also S should belong to N (set of non-terminal symbols), which implies that S is a subset of N

All of this looks very complicated. Do we really need to build all of it just to perform a simple task that might not even require everything?
NO!